how sin is computed?
I can recall the first time I wrote a program that used a trigonometric function - it was back in secondary school. I was making a game and wanted to make some object float around another. Back then, I didn’t know what trig functions were and how they worked, so I copied some code from the web and, to my astonishment, it worked. I got curious how these functions worked, so I pressed F3 in my IDE and tried to look for the source code of Math.sin. I can’t remember whether I found the code and didn’t understand it or whether I couldn’t find the implementation at all. It doesn’t really matter. What dose, is that back then I swore to myself that one day I will implement my own sin function. Two days ago, I’ve learned about Taylor Series.
Taylors, how do they work?
Taylor series is a tool to express some function as a polynomial, using its nth derivative. Since sin(x) and its derivatives are differentiable, we can express f(x) = sin(x) as:
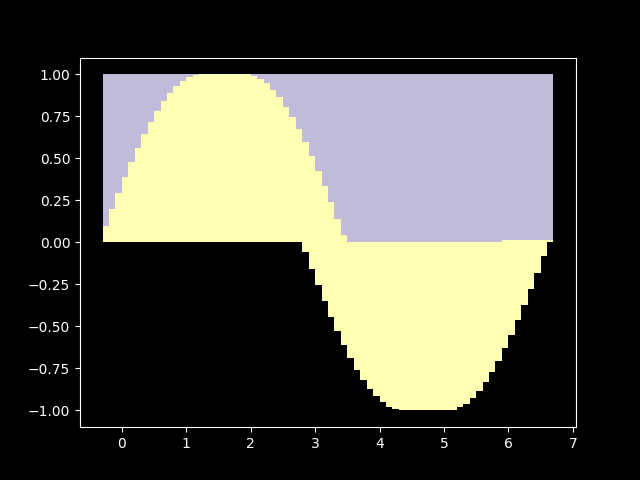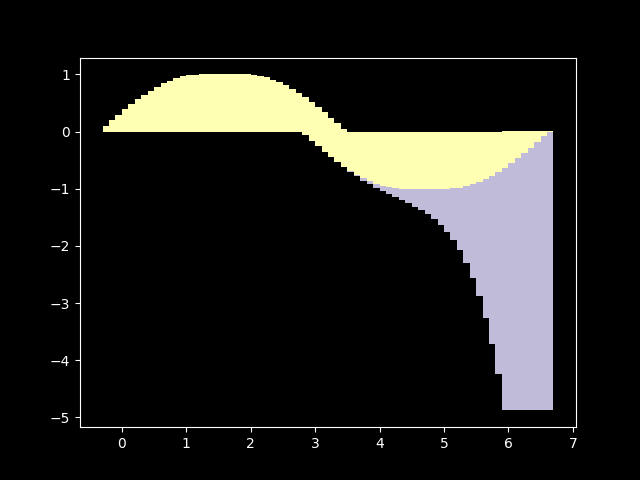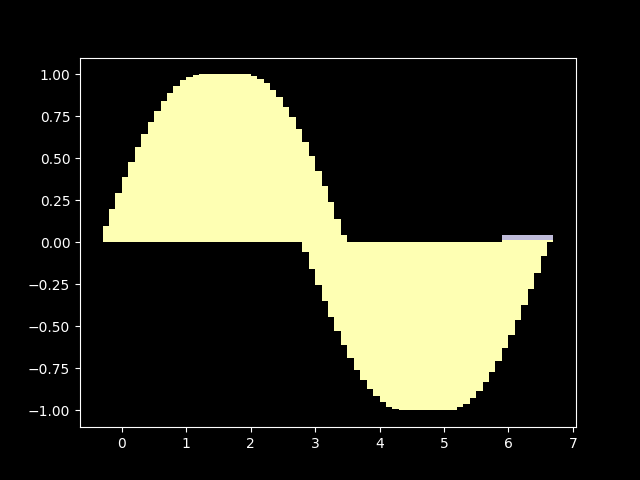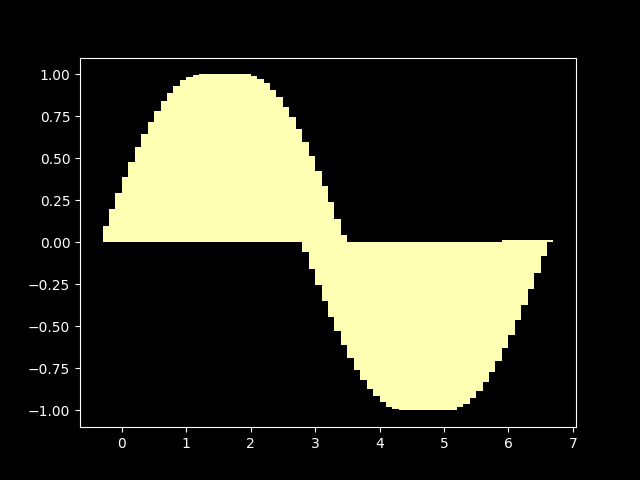
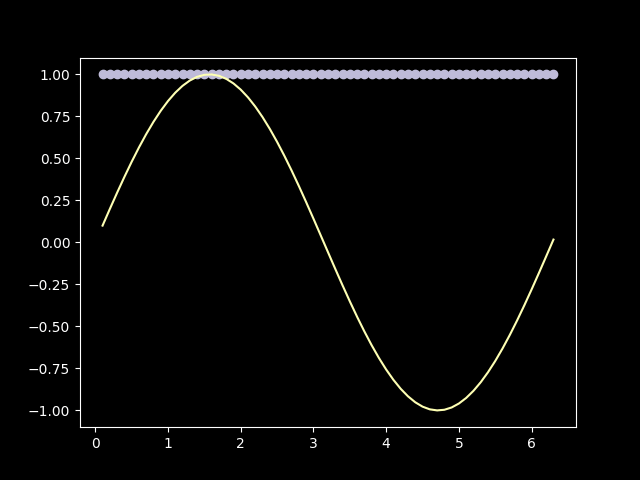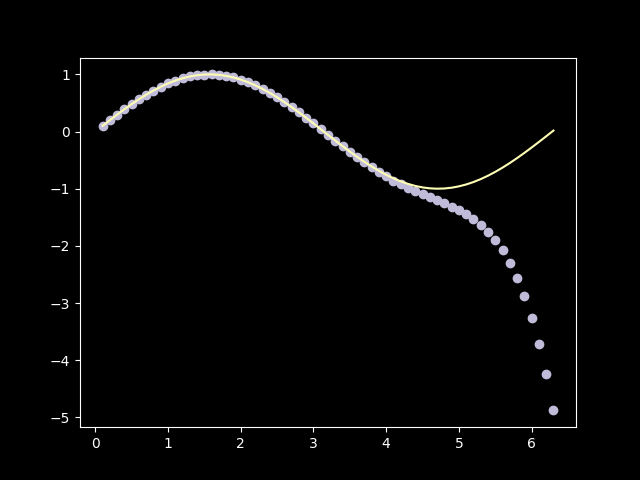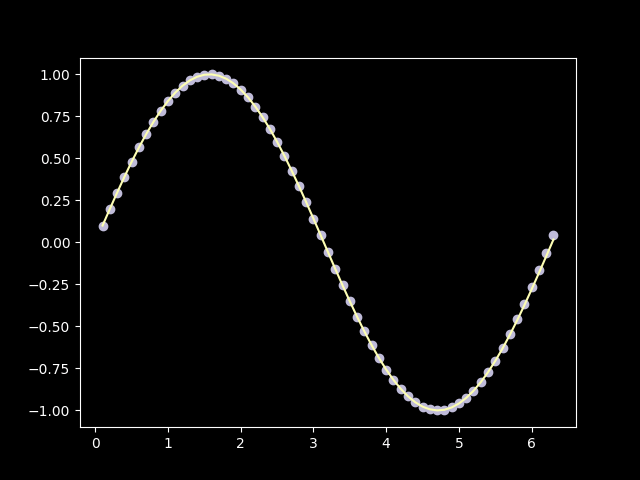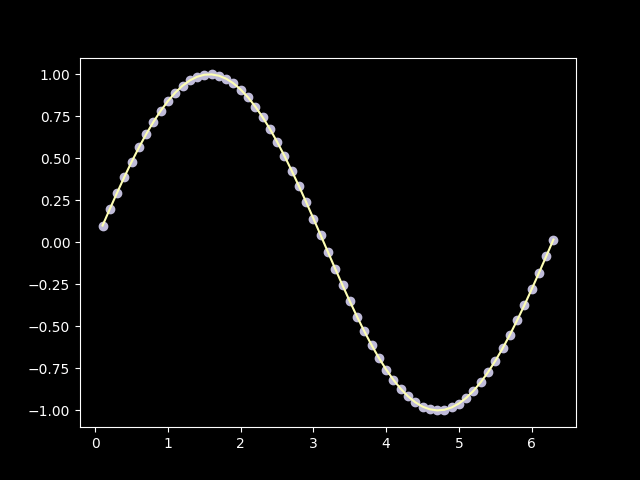
In this case, we can’t add infinitely many terms in a finite amount of time, so we have to approximate. Since this is a toy implementation, we will just compare it with python’s math.sin implementation and call it quits when they will converge good enough.
Implementation
First, we need some way of obtaining the nth derivative of sin, evaluated at some center a. By writing down sin’s first fifteen derivatives, we can see that the odd derivatives are either 1 * cos(x) or (-1) * cos(x), while the plural ones take the form of 1 * sin(x) or (-1) * sin(x). What is more difficult to see, is that derivatives with an ordinal that yields a reminder of two or three when divided by four are the derivatives with and minus sign. I don’t know how to formally prove it... yet, but you need to trust me on this one. Translating into python code:
def nth_sin_derivative(n, a=math.pi/2):
if n % 4 in (2,3):
sign = -1
else:
sign = 1
if n % 2 == 0:
function = sin
else:
function = cos
return sign * function(a)Second, we need to actually be able to evaluate both cos(x) and sin(x) at our center. Since we are implementing sin(x), we should deal with cos(x) first. We don’t have to implement cos(x) separately - notice that sin(π⁄2 - x) = cos(x):
def cos(x):
return sin((math.pi/2) - x)Great. That solves the cos(x) part. Now, we can finally implement sin(x):
def sin(x, center=math.pi/2, term_count=5):
if x == math.pi/2:
return 1
elif x == 0:
return 0
else:
values = (((x - center)**i / math.factorial(i)) * nth_sin_derivative(i, a=center) for i in range(term_count))
return sum(values)We specify two special cases: x = π⁄2 for evaluating sin derivatives that require to compute sin(x) at center, and x = 0 for evaluating sin derivatives that require to compute cos(x) at center. Else, we compute the Taylor series.
Is the implementation any good?
Well, it sure can compute sin(x)! With term_count=19 the approximation is nearly as good as the python’s math.sin:
However, assemblies actually provide an fsin instruction, so computing sin(x) in software when speed matters is kinda cringe. On the side note, CPUs don’t actually use a Taylor series to compute trig functions - they use CORDIC.